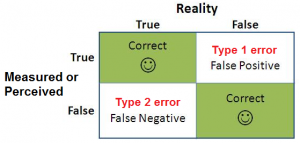
Type 1 vs Type 2 Error.
People can make mistakes when they perform a hypothesis test with statistical analysis. Specifically, they can make Type 1 vs Type 2 Errors.
As the data are analyzed and hypotheses are tested, understanding the difference between Type I and Type II errors becomes extremely important because there is a risk of committing each type of error in each analysis. , and the amount of the risk is under our control.
So if you are testing a hypothesis about a security or quality issue that could affect people’s lives or a project that could save millions of dollars to your business, what kind of error would have more serious or more costly consequences?
Is there one type of error that is more important to control than another?
Table of Contents
The null hypothesis and Type 1 vs Type 2 Error
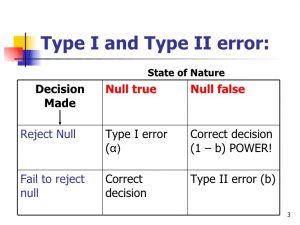Before we try to answer this question, let’s review what these errors are.
When the statistics refer to Type I and Type II errors, we refer to the two ways in which errors can be made concerning the null hypothesis (Ho). The null hypothesis is the default position, similar to the idea of ”innocence until guilt is proven.” Any hypothesis test begins with the assumption that the null hypothesis is correct.
We make a Type I error if we reject the null hypothesis when it is true. It is a false positive, like a fire alarm that sounds when there is no such fire.
A Type II error occurs if we make a mistake in rejecting the null when it is not true. It is the case of a false negative-like an alarm that fails and does not sound when there is a fire.
Reduce the risk of statistical errors
Statistics refer to the risk or likelihood of an alpha-type “alpha error,” as well as a “level of significance.” In other words, it is the willingness to reject the null hypothesis if it is correct. Alpha is usually set to 0.05, which represents a 5% chance of rejecting the null hypothesis if it is true.
The lower the alpha, the lower the probability of inaccurate deviation of the null hypothesis. For example, in situations of life or death, Alpha 0.01 reduces the probability of Type I error to only 1%.
Type II error refers to the concept of “performance,” and the probability of this error is called “beta.” We can reduce the risk of a type II error by making sure that there is enough energy in our test. It depends on whether the sample size is large enough to detect the difference if it exists.
The standard argument for “which error is worse”
Let us return to the question of which type I or type II error is worse. An example of a reference to help people think about a subject is an accused of a crime that requires a very harsh sentence.
The null hypothesis states that the accused is innocent. Of course, you do not want to release the guilty from prison, but most people will say that the conviction of an innocent person for such punishment is even worse.
Therefore, many texts and instructors will say that Type I (false positive) is worse than a Type II error (false negative). The reason is reduced to the idea that if the status quo or default assumption is maintained, at least it will not be making things worse.
And in many cases, that is true. But as it happens so much in statistics, in the application nothing is so white or black. The analogy of the accused is perfect for teaching the concept, but when you try to make a golden rule about what kind of error is worse in practice, it crumbles.
But then, what kind of error is the worst?
Sorry to be disappointed, but, as in many things in life and statistics, the most honest answer to this question should be: “It depends.”
In some situations, a Type I error may be less acceptable than a Type 2 error. In other cases, a Type II error may be less expensive than a Type I error, and sometimes, like Dan Smith, Six years ago Sigma and quality improvement said: “No” is the only answer in which the worst error is:
Most students use the concepts of Six Sigma, which they study in a business context. In business, if you pay a company $ 3 million, you offer an alternative process, if there is nothing wrong with the current process, or you do not take into account a profit of $ 3 million when you switch to a new process. But you’re mistaken. The end result is the same. The company loses the opportunity to get an additional cost of $ 3 million.
Look at the potential consequences
Since there is no clear rule of thumb on which types of errors, type I or type II, are worse, using the data to test the hypothesis is best to use the consequences that may follow two types of errors.
Several experts suggest using a table similar to the following to detail the consequences of a Type I and Type II error in a particular analysis.
Regardless of what the analysis involves, it is always wise to understand the difference between type I and type II errors and to properly deal with and mitigate the associated risks. For each error, make sure that it is.
